Balancing of a Single Rotating Mass By Two Masses Rotating in Different Planes

          In the previous article we have discussed that by introducing a single balancing mass in the same plane of rotation as that of disturbing mass, the centrifugal forces are balanced. These two forces are equal in magnitude and opposite in direction. but this type of arrangement for balancing gives rise to a couple which tends to rock the shaft in its bearing. Therefore in order to put the system in complete balance, two balancing masses are placed in two different planes, parallel to the plane of rotation of the disturbing mass, in such a way that they satisfy the following two conditions of equilibrium. 

1. The net dynamic force acting on the shaft is equal to zero. This requires that the line of action of three centrifugal forces must be the same. In other words the centre of the masses of the system must lie on the axis of rotation. This is the condition for Static Balancing.

2. The net couple due to the dynamic forces acting on the shaft equal to zero. In other words, the algebraic sum of the moments about any point in the plane must be zero.

          The above conditions (1) and (2) together gives Dynamic Balancing. The following two possibilities may arise while attaching the two balancing masses:

1. The plane of the disturbing mass may be in between the planes of the two balancing masses, and

2. The plane of the disturbing mass may lie on the left or right of the two planes containing the balancing masses.

We shall now discuss both the above cases one by one.

1. When the plane of the disturbing mass lies in between the planes of the two balancing masses:

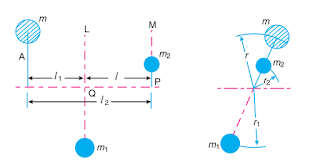
          Consider a disturbing mass 'm' lying in a plane 'A' to be balanced by two rotating masses m₁ and m₂ lying in two different planes 'L' and 'M' as shown in Fig., Let r, r₁ and r₂ be the radii of rotation of the masses in planes A, L and M respectively.

           Let        l₁ = Distance between the planes A and L,

                         l₂ =  Distance between the planes A and M, and

                         l = Distance between the planes L and M.

     We know that the centrifugal force exerted by the mass 'm' in the plane 'A',

                                   F_C = m . r . ω²

     Similarly, the centrifugal force exerted by the mass 'm₁' in the plane 'L',

                                   F_{C 1} = m₁ . r₁ . ω²

     and, the centrifugal force exerted by the mass 'm2' in the plane 'M', 

                                   F_C2 = m₂ . r₂ . ω²

          Since the net force acting on the shaft must be equal to zero, therefore the centrifugal force on the disturbing mass must be equal to the sum of the centrifugal forces on the balancing masses, therefore

                                                F_C = F_{C 1} + F_C2

                                             m . r = m₁ . r₁ + m₂ . r_{2      ..... (1)}

          Now in order to find the magnitude of balancing force in the plane 'L', take moments about 'P' which is the point of intersection of the plane 'M' and the axis of rotation. Therefore

                                               F_{C 1} X l = F_C X l₂

                                             m₁ . r₁ . l = m . r . l_{2             ...... (2)}

          Similarly, in order to find the balancing force in plane 'M', take moments about 'Q' which is the point of intersection of the plane 'L' and the axis of rotation. Therefore

                                               F_C2 X l = F_C X l₁

                                           m₂ . r₂ . l = m . r . l_{1              ........ (3)}

The equation (1) represents the condition for static balance, but in order to achieve dynamic balancing, equations (2) and (3) must also be satisfied.

2. When the plane of the disturbing mass lies on one end of the planes of the balancing masses:

          In this case, the mass 'm' lies in the plane 'A' and the balancing masses lie in the planes 'L' and 'M', as shown in Fig., As discussed above, the following conditions must be satisfied in order to balance the system, i.e., 

                                              F_C + F_C2 = F_{C 1} + F_C2

                                     m . r + m₂ . r₂ = m₁ . r₁ + m₂ . r_{2        ..... (4)}

          Now, to find the balancing force in the plane 'L', take moments about 'P' which is the point of intersection of the plane 'M' and the axis of rotation. Therefore

                                               F_{C 1} X l = F_C X l₂

                                             m₁ . r₁ . l = m . r . l_{2             ...... (5)}

          Similarly, to find the balancing force in the plane 'M', take moments about 'Q' which is the point of intersection of the plane 'L' and the axis of rotation. Therefore

                                               F_C2 X l = F_C X l₁

                                           m₂ . r₂ . l = m . r . l_{1              ........ (6)}